Conditional Features

When optimizing chemical processes, we often have some inputs that are dependent on others. For example, the value of a catalyst_concentration input feature is only relevant depending on another feature use_catalyst==True. Whilst it may seem that use_catalyst==False is equivalent to just setting catalyst_concentration==0, there may be some limitations to this approach: - If a catalyst is used, there may be some minimum amount required. It is difficult to model the disjoint bounds of a continuous feature. - It may be the case that some tiny presence of catalyst enables a side reaction that completely changes the reaction. We therefore have a step change at 0, with smoother behaviour everywhere else in the domain, which Gaussian process surrogates cannot model well.

For a some examples of literature on these problems, see [Swersky2014Arc] and [Horn2019Wedge].

[Swersky2014Arc] Swersky et al. 2014, “Raiders of the Lost Architecture: Kernels for Bayesian Optimization in Conditional Parameter Spaces” arXiv [Horn2019Wedge] Horn et al. “Surrogates for hierarchical search spaces: the wedge-kernel and an automated analysis”, GECCO

We consider a test problem as described above, where we wish to optimize the yield of a reaction by controlling the temperature and catalyst concentration.

from bofire.data_models.constraints.api import NonZeroCondition
from bofire.data_models.domain.api import Domain
from bofire.data_models.features.api import ContinuousInput, ContinuousOutput
from bofire.data_models.kernels.api import RBFKernel, WedgeKernel


catalyst_domain = Domain.from_lists(
    inputs=[
        ContinuousInput(key="temperature", unit="°C", bounds=(50.0, 100.0)),
        ContinuousInput(key="catalyst_concentration", unit="M", bounds=(0.2, 1.0), allow_zero=True),
    ],
    outputs=[ContinuousOutput(key="yield")],
)

indicator_kernel = WedgeKernel(
    base_kernel=RBFKernel(),
    conditions=[
        ("catalyst_concentration", "catalyst_concentration", NonZeroCondition())
    ],
)

After defining the domain, we can then build the wedge kernel for our GP surrogate.

from bofire.data_models.kernels.api import RBFKernel, WedgeKernel
# here, we manually build the list of conditions
# in future we will automatically build them from any inputs with allow_zero==True
conditions = [
    (
        "catalyst_concentration",
        "catalyst_concentration",
        NonZeroCondition(),
    )
]

wedge_kernel_data_model = WedgeKernel(
    base_kernel=RBFKernel(),
    conditions=conditions,
)
import torch

import bofire.kernels.api as kernels


def features_to_idx_mapper(feats: list[str]) -> list[int]:
    return catalyst_domain.inputs.get_feature_indices({}, feats)


wedge_kernel = kernels.map(
    wedge_kernel_data_model,
    batch_shape=torch.Size([]),
    active_dims=list(range(2)),
    features_to_idx_mapper=features_to_idx_mapper,
)
# cast the return type from `kernels.map` to the wedge kernel
# this fixes syntax highlighting in this notebook
from typing import cast

from bofire.kernels.conditional import WedgeKernel as WedgeKernelFunctional

wedge_kernel = cast(WedgeKernelFunctional, wedge_kernel)
wedge_kernel
WedgeKernel(
  (raw_lengthscale_constraint): Positive()
  (raw_angle_constraint): Interval(1.000E-04, 9.999E-01)
  (raw_radius_constraint): Positive()
  (base_kernel): RBFKernel(
    (raw_lengthscale_constraint): Positive()
  )
)

We check below that the kernel behaves as expected. Specifically, we want to check that the indicator function correctly masks the conditional feature to be inactive when the condition is not met.

# check the order of dimensions in X
assert features_to_idx_mapper(["catalyst_concentration", "temperature"]) == [0, 1]

X = torch.tensor(
    [
        [0.0, 0.0],
        [0.05, 0.0],
        [0.50, 0.6],
    ]
)

# the indicator function shows which dimensions are active
# X[:, 1] should always be active
# X[:, 0] should only be active if X[:, 0] != 0
wedge_kernel.indicator_func(X)
tensor([[False,  True],
        [ True,  True],
        [ True,  True]])

Using the wedge kernel for Bayesian optimizaiton

Using the domain defined at the start of the notebook, we now create a benchmark that we can use to evaluate how well this kernel works for Bayesian optimization.

We set up our objective function such that adding a catalyst enables a side reaction, and so any small prescence of the catalyst hurts yield. However, at higher concentration of catalyst, we see improved performance.

Increasing temperature increases the yield, however it also causes decomposition of the catalyst at high temperatures.

import numpy as np
import pandas as pd

from bofire.benchmarks.api import Benchmark


class ReactionOptimizationBenchmark(Benchmark):
    _domain = catalyst_domain

    def _f(self, X: pd.DataFrame, **kwargs) -> pd.DataFrame:  # type: ignore
        cat_conc = X["catalyst_concentration"]
        temp = X["temperature"]
        norm_temp = (temp - 50) / 50

        side_product = np.where(cat_conc > 0.0, 10.0, 0.0)
        effective_catalyst = np.clip(cat_conc - 1.5 * (norm_temp - 0.5), 0.0, cat_conc)

        catalyst_effect = 10 * np.exp(effective_catalyst)
        temperature_effect = 10 * np.exp(norm_temp)
        y = temperature_effect + catalyst_effect - side_product

        Y = pd.DataFrame({"yield": y, "valid_yield": 1})
        return Y


benchmark = ReactionOptimizationBenchmark()

First, we plot the objective function:

import matplotlib.pyplot as plt


N_grid_pts = 50
# plot active points
X_c, X_t = np.meshgrid(
    np.linspace(0.5, 1.0, num=N_grid_pts), np.linspace(50, 100, num=N_grid_pts)
)
grid_X = np.stack((X_c.flatten(), X_t.flatten()), axis=-1)
grid_Y = benchmark.f(
    pd.DataFrame(data=grid_X, columns=["catalyst_concentration", "temperature"])
)["yield"].to_numpy()
plt.contourf(X_c, X_t, grid_Y.reshape(N_grid_pts, N_grid_pts), vmin=10, vmax=40)

# plot inactive points
X_c, X_t = np.meshgrid(
    np.linspace(-0.05, 0.05, num=2), np.linspace(50, 100, num=N_grid_pts)
)
grid_X = np.stack((0.0 * X_c.flatten(), X_t.flatten()), axis=-1)
grid_Y = benchmark.f(
    pd.DataFrame(data=grid_X, columns=["catalyst_concentration", "temperature"])
)["yield"].to_numpy()
plt.contourf(X_c, X_t, grid_Y.reshape(N_grid_pts, 2), vmin=10, vmax=40)

plt.colorbar()
plt.xlabel("catalyst_concentration")
plt.ylabel("temperature")
Text(0, 0.5, 'temperature')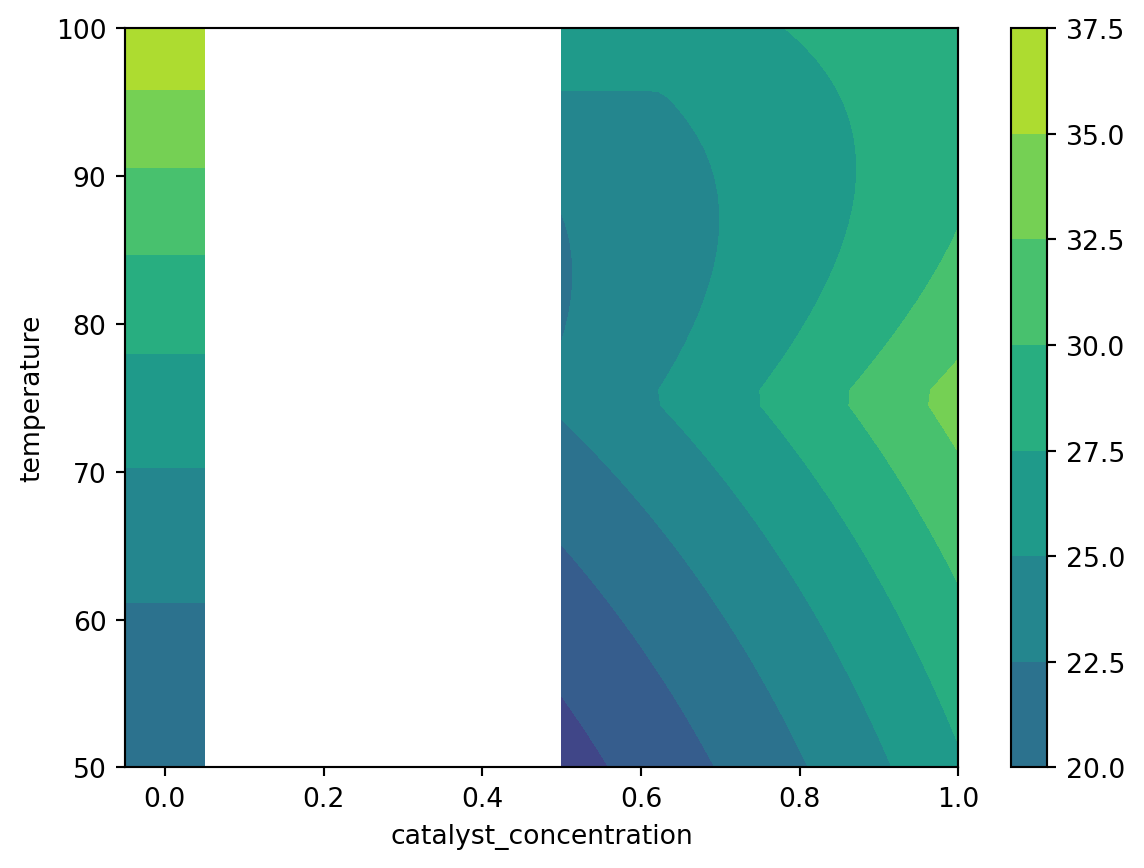

import bofire.strategies.api as strategies
from bofire.data_models.strategies.api import RandomStrategy, SoboStrategy


samples = strategies.map(RandomStrategy(domain=catalyst_domain, seed=0)).ask(10)
# RandomStrategy doesn't currently support randomly sampling with allow_zero
# So we manually set the first 2 reactions to have no catalyst.
samples.loc[:1, "catalyst_concentration"] = 0.0
experiments = benchmark.f(samples, return_complete=True)
experiments.head(4)
catalyst_concentration temperature yield valid_yield
0 0.000000 59.171060 22.013203 1
1 0.000000 74.864291 26.442524 1
2 0.297314 92.215550 23.263744 1
3 0.406463 75.872417 21.404513 1 
from bofire.data_models.surrogates.api import BotorchSurrogates, SingleTaskGPSurrogate


sobo_strategy_data_model = SoboStrategy(
    domain=catalyst_domain,
    seed=1,
    surrogate_specs=BotorchSurrogates(
        surrogates=[
            SingleTaskGPSurrogate(
                inputs=catalyst_domain.inputs,
                outputs=catalyst_domain.outputs,
                kernel=wedge_kernel_data_model,
            )
        ]
    ),
)
strategy = strategies.map(sobo_strategy_data_model)
strategy.tell(experiments, replace=True)

We would expect the proposed batch to include some experiments with no catalyst, and some with a catalyst. Note that the volume of the search space with catalyst is larger, so we may also expect more experiments with the feature active.

strategy.ask(5)
catalyst_concentration temperature yield_pred yield_sd yield_des
0 0.920084 55.793790 29.725369 2.410661 29.725369
1 0.000000 97.313192 27.228390 3.424580 27.228390
2 1.000000 72.165219 31.275936 0.585717 31.275936
3 0.616450 50.000000 27.636364 3.372072 27.636364
4 1.000000 50.000000 28.600987 3.072161 28.600987