Getting started¶
In the following it is showed how to setup optimization problems in BoFire and how to use strategies to solve them.
Setting up the optimization problem¶
In BoFire, an optimization problem is defined by defining a domain containing input and output features as well as constraints (optional).
Features¶
Input features can be continuous, discrete, categorical, or categorical with descriptors:
from bofire.data_models.features.api import (
CategoricalDescriptorInput,
CategoricalInput,
ContinuousInput,
DiscreteInput,
)
x1 = ContinuousInput(key="x1", bounds=(0, 1))
x2 = ContinuousInput(key="x2", bounds=(0, 1))
x3 = ContinuousInput(key="x3", bounds=(0, 1))
x4 = DiscreteInput(key="x4", values=[1, 2, 5, 7.5])
x5 = CategoricalInput(key="x5", categories=["A", "B", "C"], allowed=[True, True, False])
x6 = CategoricalDescriptorInput(
key="x6",
categories=["c1", "c2", "c3"],
descriptors=["d1", "d2"],
values=[[1, 2], [2, 5], [1, 7]],
)
As output features, currently only continuous output features are supported. Each output feature should have an objective, which can be a minimize or maximize objective. Furthermore, we can define weights between 0 and 1 in case the objectives should not be weighted equally.
from bofire.data_models.features.api import ContinuousOutput
from bofire.data_models.objectives.api import MaximizeObjective, MinimizeObjective
objective1 = MaximizeObjective(
w=1.0,
bounds=[0.0, 1.0],
)
y1 = ContinuousOutput(key="y1", objective=objective1)
objective2 = MinimizeObjective(w=1.0)
y2 = ContinuousOutput(key="y2", objective=objective2)
In- and output features are collected in respective feature lists.
from bofire.data_models.domain.api import Inputs, Outputs
input_features = Inputs(features=[x1, x2, x3, x4, x5, x6])
output_features = Outputs(features=[y1, y2])
A summary of the constraints can be obtained by the method get_reps_df:
input_features.get_reps_df()
output_features.get_reps_df()
Individual features can be retrieved by name.
x5 = input_features.get_by_key("x5")
x5
This is also possible with list of feature names.
input_features.get_by_keys(["x5", "x2"])
Features of a specific type can be returned by the get method, by default it returns all features that are an instance of the provided class.
input_features.get(CategoricalInput)
By using the exact argument one can force it to only return feature of the exact same class.
input_features.get(CategoricalInput, exact=True)
The get_keys method follows the same logic as the get method but returns just the keys of the features instead of the features itself.
input_features.get_keys(CategoricalInput)
The input feature container further provides methods to return a feature container with only all fixed or all free features.
free_inputs = input_features.get_free()
fixed_inputs = input_features.get_fixed()
One can uniformly sample from individual input features.
x5.sample(2)
Or directly from input feature containers, uniform, sobol and LHS sampling is possible. A default, uniform sampling is used.
from bofire.data_models.enum import SamplingMethodEnum
X = input_features.sample(n=10, method=SamplingMethodEnum.LHS)
X
Constraints¶
The search space can be further defined by constraints on the input features. BoFire supports linear equality and inequality constraints, as well as non-linear equality and inequality constraints.
Linear constraints¶
LinearEqualityConstraint and LinearInequalityConstraint are expressions of the form $\sum_i a_i x_i = b$ or $\leq b$ for equality and inequality constraints respectively.
They take a list of names of the input features they are operating on, a list of left-hand-side coefficients $a_i$ and a right-hand-side constant $b$.
from bofire.data_models.constraints.api import (
LinearEqualityConstraint,
LinearInequalityConstraint,
)
# A mixture: x1 + x2 + x3 = 1
constr1 = LinearEqualityConstraint(
features=["x1", "x2", "x3"],
coefficients=[1, 1, 1],
rhs=1,
)
# x1 + 2 * x3 < 0.8
constr2 = LinearInequalityConstraint(
features=["x1", "x3"],
coefficients=[1, 2],
rhs=0.8,
)
Linear constraints can only operate on ContinuousInput features.
Nonlinear constraints¶
NonlinearEqualityConstraint and NonlinearInequalityConstraint take any expression that can be evaluated by pandas.eval, including mathematical operators such as sin, exp, log10 or exponentiation. So far, they cannot be used in any optimizations.
from bofire.data_models.constraints.api import NonlinearEqualityConstraint
# The unit circle: x1**2 + x2**2 = 1
const3 = NonlinearEqualityConstraint(expression="x1**2 + x2**2 - 1")
const3
Combinatorial constraint¶
Use NChooseKConstraint to express that we only want to have $k$ out of the $n$ parameters to take positive values.
Think of a mixture, where we have long list of possible ingredients, but want to limit number of ingredients in any given recipe.
from bofire.data_models.constraints.api import NChooseKConstraint
# Only 2 or 3 out of 3 parameters can be greater than zero
constr5 = NChooseKConstraint(
features=["x1", "x2", "x3"],
min_count=2,
max_count=3,
none_also_valid=True,
)
constr5
Note that we have to set a boolean, if None is also a valid selection, e.g. if we want to have 2 or 3 or none of the ingredients in our recipe.
Similar to the features, constraints can be grouped in a container which acts as the union constraints.
from bofire.data_models.domain.api import Constraints
constraints = Constraints(constraints=[constr1, constr2])
A summary of the constraints can be obtained by the method get_reps_df:
constraints.get_reps_df()
We can check whether a point satisfies individual constraints or the list of constraints.
constr2.is_fulfilled(X).values
Output constraints can be setup via sigmoid-shaped objectives passed as argument to the respective feature, which can then also be plotted.
from bofire.data_models.objectives.api import MinimizeSigmoidObjective
from bofire.plot.api import plot_objective_plotly
output_constraint = MinimizeSigmoidObjective(w=1.0, steepness=10, tp=0.5)
y3 = ContinuousOutput(key="y3", objective=output_constraint)
output_features = Outputs(features=[y1, y2, y3])
fig = plot_objective_plotly(feature=y3, lower=0, upper=1)
fig.show()
The domain¶
The domain holds then all information about an optimization problem and can be understood as a search space definition.
from bofire.data_models.domain.api import Domain
domain = Domain(inputs=input_features, outputs=output_features, constraints=constraints)
In addition one can instantiate the domain also just from lists.
domain_single_objective = Domain.from_lists(
inputs=[x1, x2, x3, x4, x5, x6],
outputs=[y1],
constraints=[],
)
Optimization¶
To solve the optimization problem, we further need a solving strategy. BoFire supports strategies without a prediction model such as a random strategy and predictive strategies which are based on a prediction model.
All strategies contain an ask method returning a defined number of candidate experiments.
Random Strategy¶
import bofire.strategies.api as strategies
from bofire.data_models.strategies.api import RandomStrategy
strategy_data_model = RandomStrategy(domain=domain)
random_strategy = strategies.map(strategy_data_model)
random_candidates = random_strategy.ask(2)
random_candidates
Single objective Bayesian Optimization strategy¶
Since a predictive strategy includes a prediction model, we need to generate some historical data, which we can afterwards pass as training data to the strategy via the tell method.
For didactic purposes we just choose here from one of our benchmark methods.
from bofire.benchmarks.single import Himmelblau
benchmark = Himmelblau()
(benchmark.domain.inputs + benchmark.domain.outputs).get_reps_df()
Generating some initial data works as follows:
samples = benchmark.domain.inputs.sample(10)
experiments = benchmark.f(samples, return_complete=True)
experiments
Let's setup the SOBO strategy and ask for a candidate.
from bofire.data_models.acquisition_functions.api import qLogNEI
from bofire.data_models.strategies.api import SoboStrategy
sobo_strategy_data_model = SoboStrategy(
domain=benchmark.domain,
acquisition_function=qLogNEI(),
)
sobo_strategy = strategies.map(sobo_strategy_data_model)
sobo_strategy.tell(experiments=experiments)
sobo_strategy.ask(candidate_count=1)
Design of Experiments¶
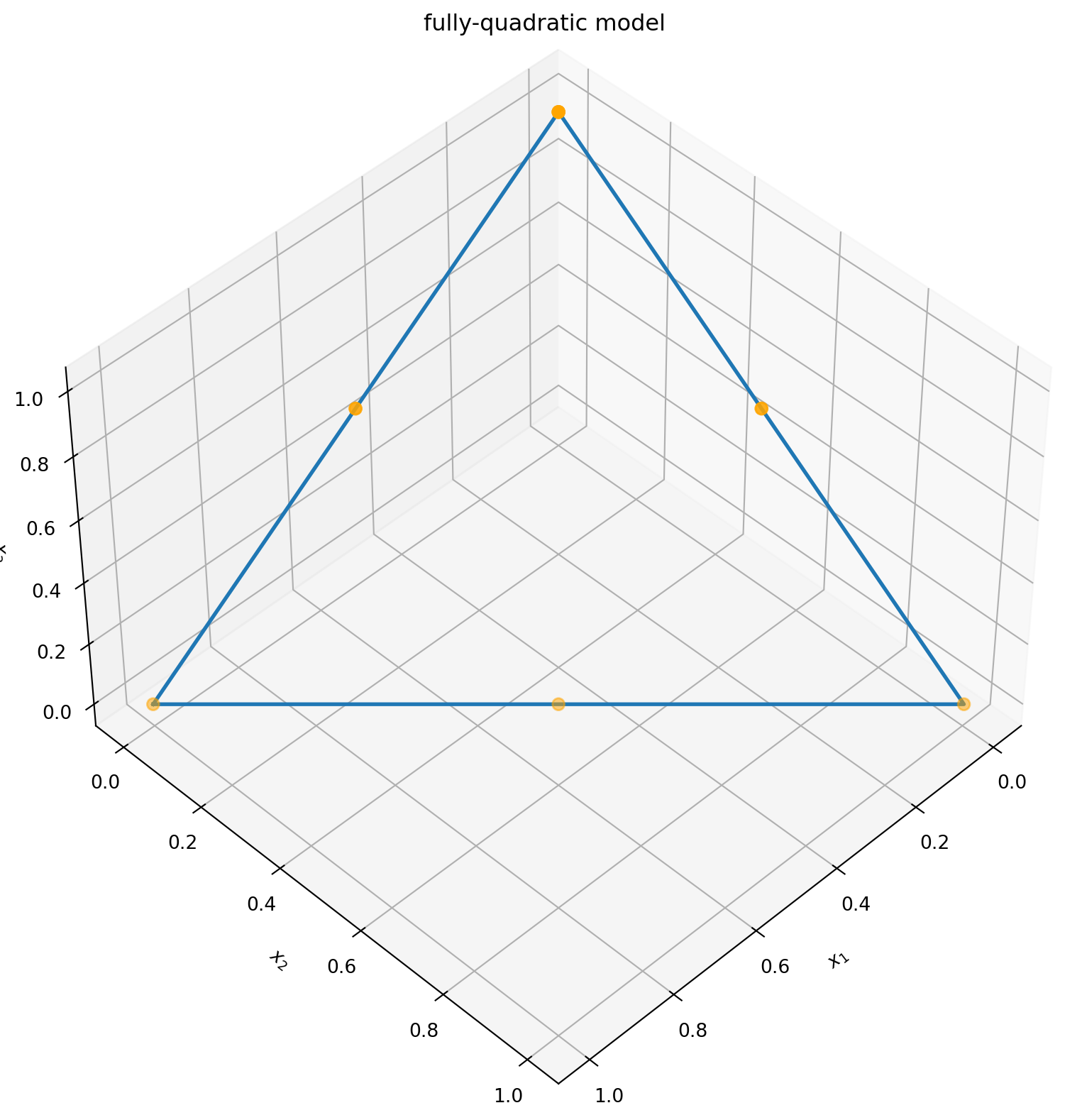
As a simple example for the DoE functionalities we consider the task of finding a D-optimal design for a fully-quadratic model with three design variables with bounds (0,1) and a mixture constraint.
We define the design space including the constraint as a domain. Then we pass it to the optimization routine and specify the model. If the user does not indicate a number of experiments it will be chosen automatically based on the number of model terms.
import numpy as np
from bofire.strategies.doe.design import find_local_max_ipopt
domain = Domain(inputs=[x1, x2, x3], outputs=[y1], constraints=[constr1])
res = find_local_max_ipopt(domain, "fully-quadratic")
np.round(res, 3)
The resulting design looks like this:
import matplotlib.pyplot as plt
fig = plt.figure(figsize=((10, 10)))
ax = fig.add_subplot(111, projection="3d")
ax.view_init(45, 45)
ax.set_title("fully-quadratic model")
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$x_3$")
plt.rcParams["figure.figsize"] = (10, 8)
# plot feasible polytope
ax.plot(xs=[1, 0, 0, 1], ys=[0, 1, 0, 0], zs=[0, 0, 1, 0], linewidth=2)
# plot D-optimal solutions
ax.scatter(xs=res["x1"], ys=res["x2"], zs=res["x3"], marker="o", s=40, color="orange")