Design with explicit Formula

This tutorial notebook shows how to setup a D-optimal design with BoFire while providing an explicit formula and not just one of the four available keywords linear, linear-and-interaction, linear-and-quadratic, fully-quadratic.

Make sure that cyipoptis installed. The recommend way is the installation via conda conda install -c conda-forge cyipopt.

Imports

import bofire.strategies.api as strategies
from bofire.data_models.api import Domain, Inputs
from bofire.data_models.features.api import ContinuousInput
from bofire.data_models.strategies.api import DoEStrategy
from bofire.data_models.strategies.doe import DOptimalityCriterion
from bofire.utils.doe import get_confounding_matrix
/opt/hostedtoolcache/Python/3.12.14/x64/lib/python3.12/site-packages/torch/jit/_script.py:1491: FutureWarning: `torch.jit.script` is deprecated. Please switch to `torch.compile` or `torch.export`.
  warnings.warn(
/opt/hostedtoolcache/Python/3.12.14/x64/lib/python3.12/site-packages/torch/jit/_script.py:1491: FutureWarning: `torch.jit.script` is deprecated. Please switch to `torch.compile` or `torch.export`.
  warnings.warn(

Setup of the problem

input_features = Inputs(
    features=[
        ContinuousInput(key="a", bounds=(0, 5)),
        ContinuousInput(key="b", bounds=(40, 800)),
        ContinuousInput(key="c", bounds=(80, 180)),
        ContinuousInput(key="d", bounds=(200, 800)),
    ],
)
domain = Domain(inputs=input_features)

Definition of the formula for which the optimal points should be found

model_type = "a + {a**2} + b + c + d + a:b + a:c + a:d + b:c + b:d + c:d"
model_type
'a + {a**2} + b + c + d + a:b + a:c + a:d + b:c + b:d + c:d'

Find D-optimal Design

data_model = DoEStrategy(
    domain=domain,
    criterion=DOptimalityCriterion(formula=model_type),
    ipopt_options={"max_iter": 100, "print_level": 0},
)
strategy = strategies.map(data_model=data_model)
design = strategy.ask(17)
design
/opt/hostedtoolcache/Python/3.12.14/x64/lib/python3.12/site-packages/bofire/strategies/doe/utils.py:819: OptimizeWarning: Unknown solver options: disp
  result = opt.minimize(
a b c d
0 2.398967 800.000000 180.0 800.000000
1 2.439690 40.000000 80.0 800.000000
2 5.000000 800.000000 80.0 800.000000
3 0.000000 800.000000 180.0 200.000000
4 5.000000 800.000000 180.0 637.363262
5 0.000000 40.000000 80.0 200.000000
6 0.000000 800.000000 80.0 200.000000
7 0.000000 800.000000 80.0 200.000000
8 5.000000 40.000000 80.0 800.000000
9 5.000000 800.000000 80.0 200.000000
10 5.000000 40.000000 80.0 200.000000
11 0.000000 40.000000 80.0 800.000000
12 5.000000 40.000000 180.0 800.000000
13 0.000000 402.596601 180.0 800.000000
14 5.000000 40.000000 180.0 200.000000
15 0.000000 800.000000 80.0 800.000000
16 0.000000 40.000000 180.0 200.000000

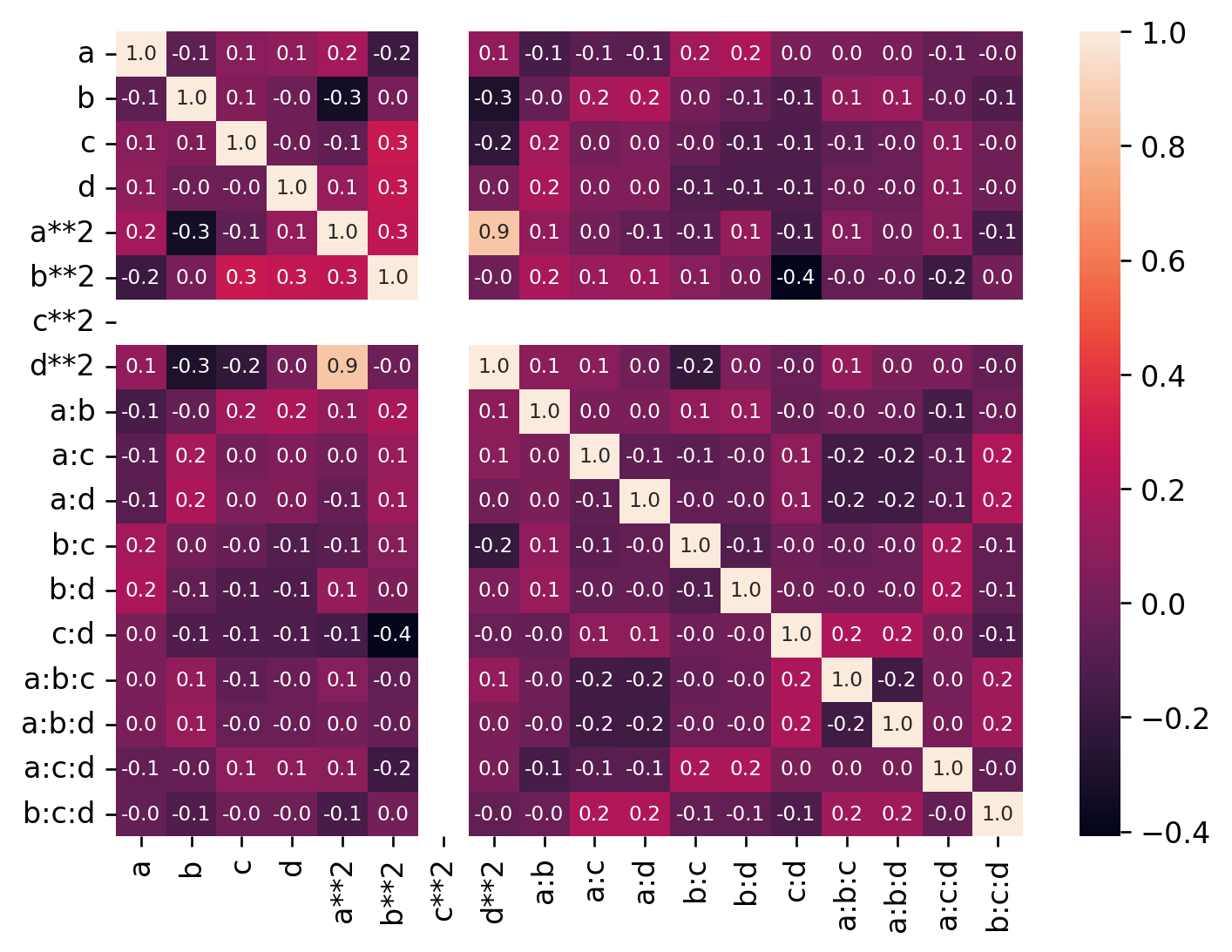
Analyze Confounding

import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns


matplotlib.rcParams["figure.dpi"] = 120

m = get_confounding_matrix(
    domain.inputs,
    design=design,
    interactions=[2, 3],
    powers=[2],
)

sns.heatmap(m, annot=True, annot_kws={"fontsize": 7}, fmt="2.1f")
plt.show()