---
title: Full and Fractional Factorial Designs
jupyter: python3
---
BoFire can be used to setup full (two level) and fractional factorial designs (https://en.wikipedia.org/wiki/Fractional_factorial_design). This tutorial notebook shows how.
## Imports and helper functions
```{python}
#| papermill: {duration: 4.584683, end_time: '2024-10-10T20:36:14.685114', exception: false, start_time: '2024-10-10T20:36:10.100431', status: completed}
#| tags: []
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import bofire.strategies.api as strategies
from bofire.data_models.domain.api import Domain
from bofire.data_models.features.api import CategoricalInput, ContinuousInput
from bofire.data_models.strategies.api import FractionalFactorialStrategy
from bofire.utils.doe import get_alias_structure, get_confounding_matrix, get_generator
def plot_design(design: pd.DataFrame):
# we do a plot with three subplots in one row in which the three degrees of freedom (temperature, time and ph) are plotted
_, axs = plt.subplots(1, 3, figsize=(15, 5))
axs[0].scatter(design["temperature"], design["time"])
axs[0].set_xlabel("Temperature")
axs[0].set_ylabel("Time")
axs[1].scatter(design["temperature"], design["ph"])
axs[1].set_xlabel("Temperature")
axs[1].set_ylabel("pH")
axs[2].scatter(design["time"], design["ph"])
axs[2].set_xlabel("Time")
axs[2].set_ylabel("pH")
plt.show()
```
## Setup the problem domain
The designs are generated for a simple three dimensional problem comprised of three continuous factors/features.
```{python}
#| papermill: {duration: 0.007239, end_time: '2024-10-10T20:36:14.698521', exception: false, start_time: '2024-10-10T20:36:14.691282', status: completed}
#| tags: []
domain = Domain(
inputs=[
ContinuousInput(key="temperature", bounds=(20, 80)),
ContinuousInput(key="time", bounds=(60, 120)),
ContinuousInput(key="ph", bounds=(7, 13)),
],
)
```
## Setup a full factorial design
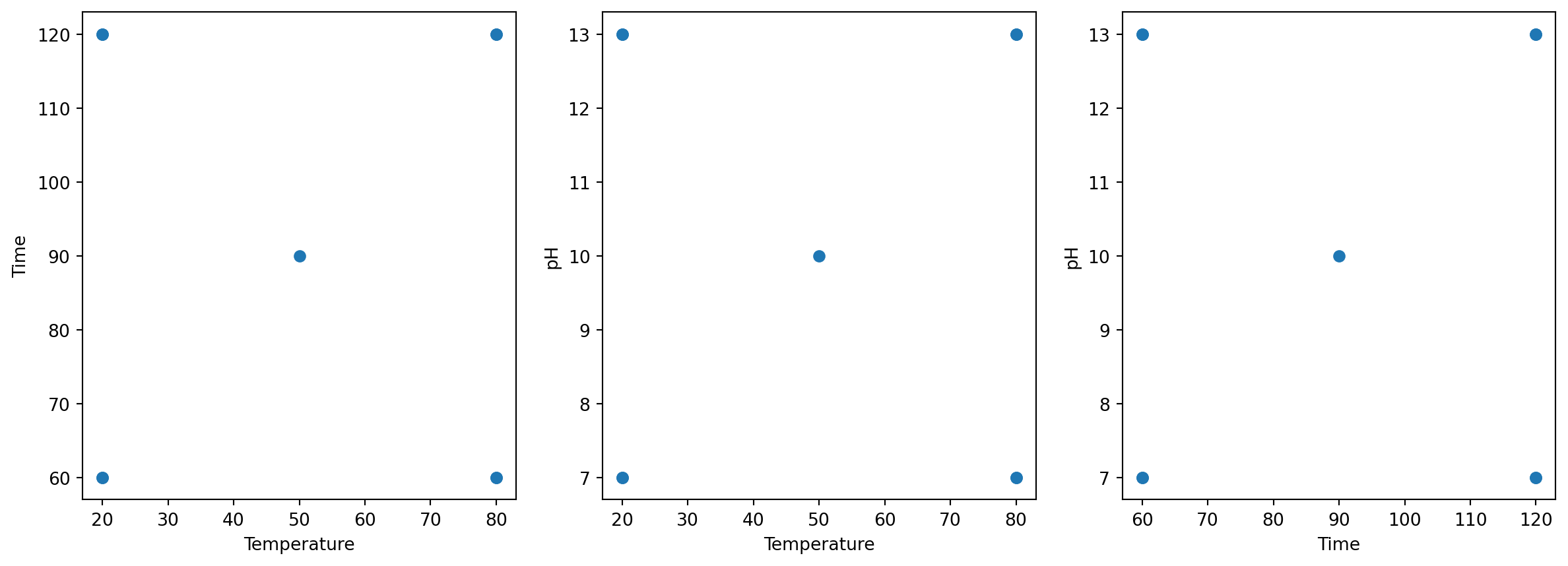
Here we setup a full two-level factorial design including a center point and plot it.
```{python}
#| papermill: {duration: 0.193231, end_time: '2024-10-10T20:36:14.897979', exception: false, start_time: '2024-10-10T20:36:14.704748', status: completed}
#| tags: []
strategy_data = FractionalFactorialStrategy(
domain=domain,
n_center=1, # number of center points
n_repetitions=1, # number of repetitions, we do only one round here
)
strategy = strategies.map(strategy_data)
design = strategy.ask()
display(design)
plot_design(design=design)
```
The confounding structure is shown below, as expected for a full factorial design, no confound is present.
```{python}
#| papermill: {duration: 0.107183, end_time: '2024-10-10T20:36:15.012084', exception: false, start_time: '2024-10-10T20:36:14.904901', status: completed}
#| tags: []
m = get_confounding_matrix(domain.inputs, design=design, interactions=[2])
sns.heatmap(m, annot=True, annot_kws={"fontsize": 7}, fmt="2.1f")
plt.show()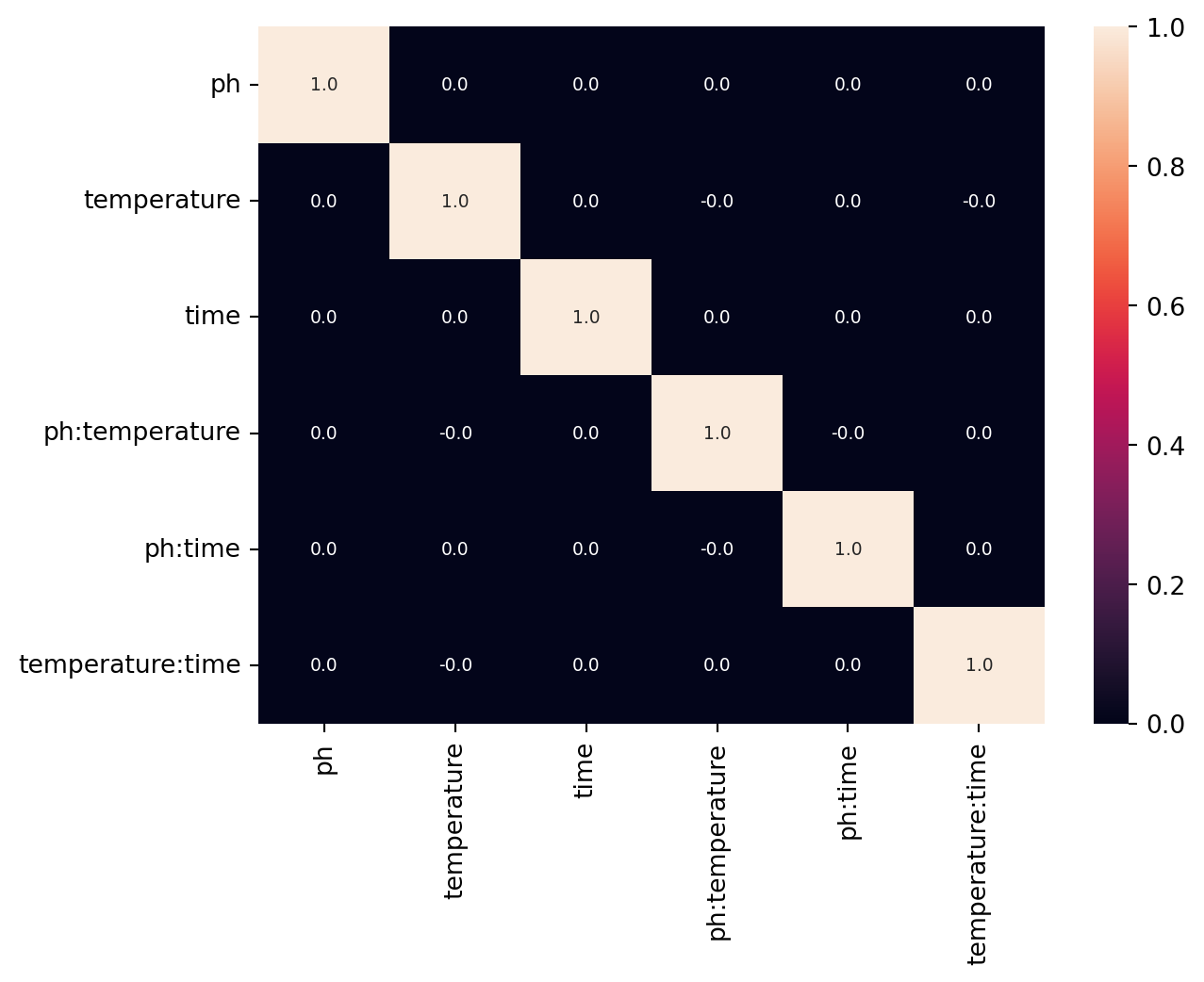
```
## Setup a full factorial design with blocking
Here we setup a blocked full two-level factorial design including a center point and plot it.
```{python}
blocked_domain = Domain(
inputs=[
ContinuousInput(key="temperature", bounds=(20, 80)),
ContinuousInput(key="time", bounds=(60, 120)),
ContinuousInput(key="ph", bounds=(7, 13)),
CategoricalInput(key="operator", categories=["A", "B", "C", "D"]),
],
)
strategy_data = FractionalFactorialStrategy(
domain=blocked_domain,
n_center=1, # number of center points per block
n_repetitions=1, # number of repetitions, we do only one round here
block_feature_key="operator",
)
strategy = strategies.map(strategy_data)
design = strategy.ask()
display(design)
plot_design(design=design)
```
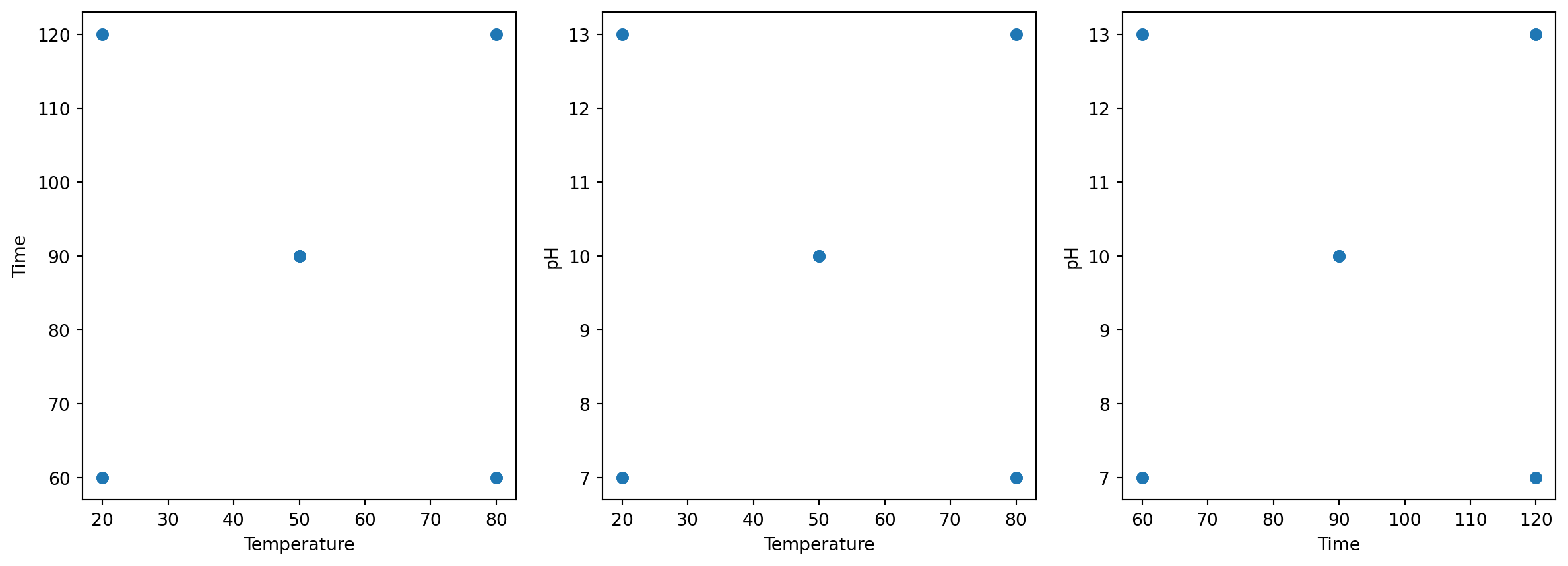
## Setup a fractional factorial design
Here a fractional factorial design of the form $2^{3-1}$ is setup by specifying the number of generators (here 1). In comparison to the full factorial design with 9 candidates, it features only 5 experiments.
```{python}
#| papermill: {duration: 0.012973, end_time: '2024-10-10T20:36:15.037263', exception: false, start_time: '2024-10-10T20:36:15.024290', status: completed}
#| tags: []
strategy_data = FractionalFactorialStrategy(
domain=domain,
n_center=1, # number of center points
n_repetitions=1, # number of repetitions, we do only one round here
n_generators=1, # number of generators, ie number of reducing factors
)
strategy = strategies.map(strategy_data)
design = strategy.ask()
display(design)
```
The generator string is automatically generated by making use of the method `get_generator` and specifying the total number of factors (here 3) and the number of generators (here 1).
```{python}
#| papermill: {duration: 0.008137, end_time: '2024-10-10T20:36:15.052737', exception: false, start_time: '2024-10-10T20:36:15.044600', status: completed}
#| tags: []
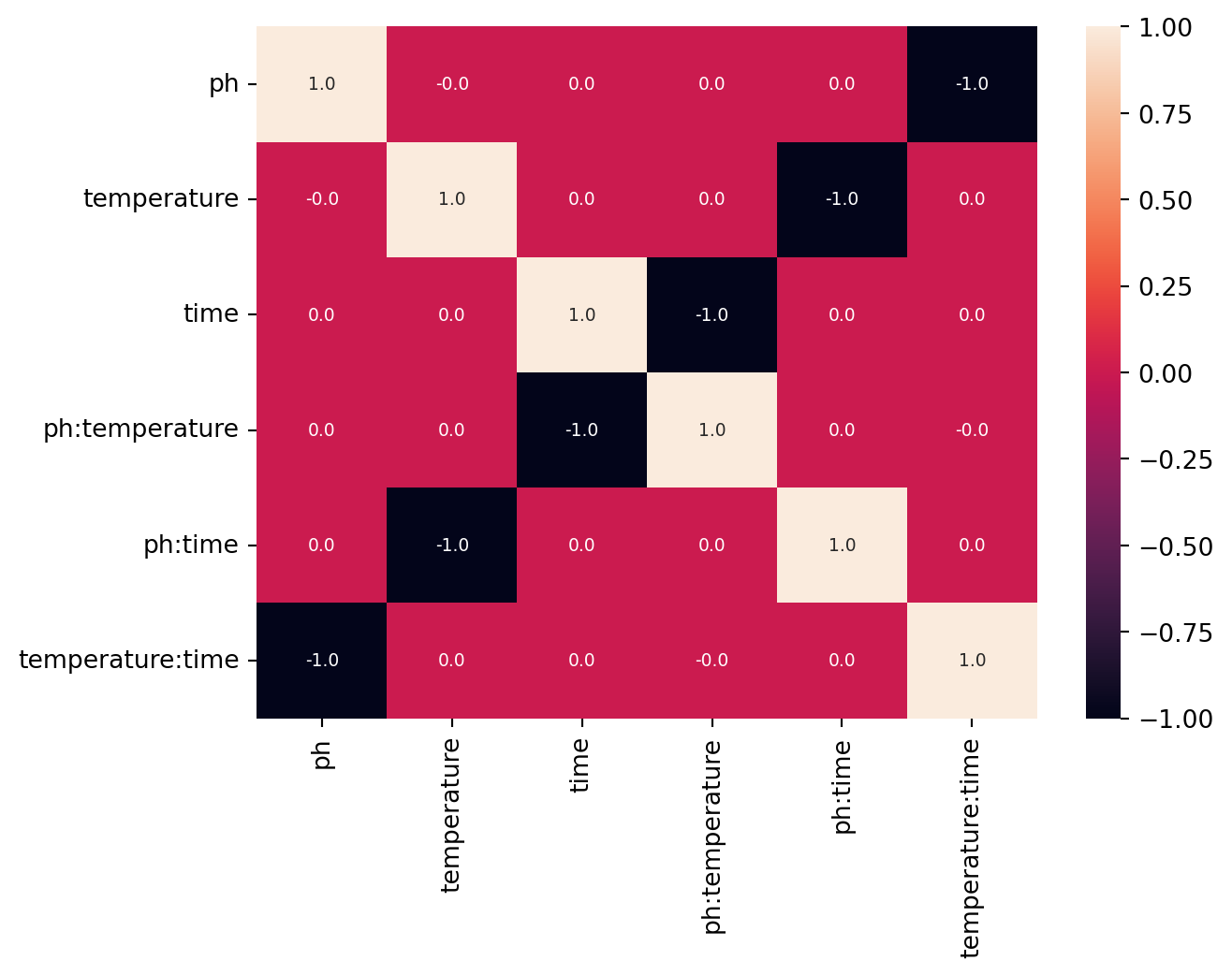
get_generator(n_factors=3, n_generators=1)
```
As expected for a type III design the main effects are confounded with the two factor interactions:
```{python}
#| papermill: {duration: 0.107571, end_time: '2024-10-10T20:36:15.168255', exception: false, start_time: '2024-10-10T20:36:15.060684', status: completed}
#| tags: []
m = get_confounding_matrix(domain.inputs, design=design, interactions=[2])
sns.heatmap(m, annot=True, annot_kws={"fontsize": 7}, fmt="2.1f")
plt.show()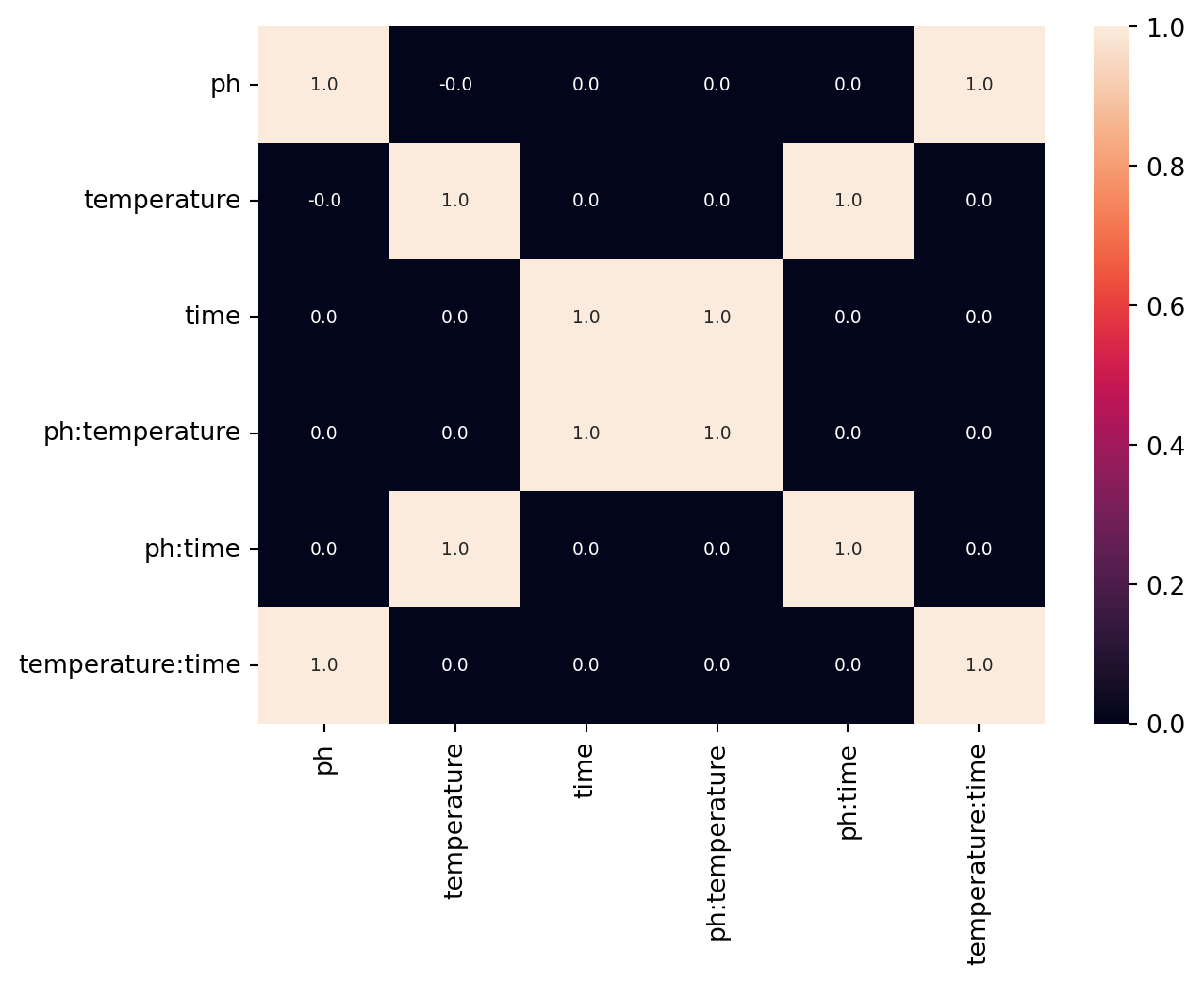
```
This can also be expressed by the so called alias structure that can be calculated as following:
```{python}
#| papermill: {duration: 0.006933, end_time: '2024-10-10T20:36:15.183147', exception: false, start_time: '2024-10-10T20:36:15.176214', status: completed}
#| tags: []
get_alias_structure("a b ab")
```
Here again a fractional factorial design of the form $2^{3-1}$ is setup by providing the complete generator string of the form `a b -ab` explicitly to the strategy.
```{python}
#| papermill: {duration: 0.012145, end_time: '2024-10-10T20:36:15.203578', exception: false, start_time: '2024-10-10T20:36:15.191433', status: completed}
#| tags: []
strategy_data = FractionalFactorialStrategy(
domain=domain,
n_center=1, # number of center points
n_repetitions=1, # number of repetitions, we do only one round here
generator="a b -ab", # the exact generator
)
strategy = strategies.map(strategy_data)
design = strategy.ask()
display(design)
```
The last two designs differ only in the last feature `time`, since the generator strings are different. In the first one it holds `time=ph x temperature` whereas in the second it holds `time=-ph x temperature`, which is also reflected in the confounding structure.
```{python}
#| papermill: {duration: 0.112252, end_time: '2024-10-10T20:36:15.324464', exception: false, start_time: '2024-10-10T20:36:15.212212', status: completed}
#| tags: []
m = get_confounding_matrix(domain.inputs, design=design, interactions=[2])
sns.heatmap(m, annot=True, annot_kws={"fontsize": 7}, fmt="2.1f")
plt.show()
```
