import matplotlib.pyplot as plt
import bofire.strategies.api as strategies
from bofire.data_models.constraints.api import LinearEqualityConstraint
from bofire.data_models.domain.api import Domain
from bofire.data_models.features.api import ContinuousInput, ContinuousOutput
from bofire.data_models.strategies.api import DoEStrategy
from bofire.data_models.strategies.doe import (
AOptimalityCriterion,
DOptimalityCriterion,
EOptimalityCriterion,
IOptimalityCriterion,
KOptimalityCriterion,
SpaceFillingCriterion,
)
from bofire.strategies.doe.objective import get_objective_functionDoE Optimality Criteria in BoFire
This tutorial notebook demonstrates the impact of different optimality-criteria for generating candidates using the DoE strategy for a two-dimensional fully-quadratic model.
Imports
Designs for different optimality criteria
# Optimal designs for a quadratic model on the unit square
domain = Domain(
inputs=[ContinuousInput(key=f"x{i+1}", bounds=(0, 1)) for i in range(2)],
outputs=[ContinuousOutput(key="y")],
)
model_type = "fully-quadratic"
n_experiments = 13
fig, ax = plt.subplots(figsize=(8, 8))
for crit, label in [
(DOptimalityCriterion, "D-Optimality"),
(AOptimalityCriterion, "A-Optimality"),
(KOptimalityCriterion, "K-Optimality"),
(EOptimalityCriterion, "E-Optimality"),
(IOptimalityCriterion, "I-Optimality"),
]:
criterion = crit(formula=model_type)
data_model = DoEStrategy(
domain=domain,
criterion=criterion,
ipopt_options={"max_iter": 300},
)
strategy = strategies.map(data_model=data_model)
design = strategy.ask(candidate_count=n_experiments)
obj_value = get_objective_function(
criterion=criterion, domain=domain, n_experiments=n_experiments
).evaluate(design.to_numpy().flatten())
ax.scatter(design.x1, design.x2, s=40, label=f"{label}")
ax.set_title("Designs with different optimality criteria")
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.grid(alpha=0.3)
ax.legend()
plt.show()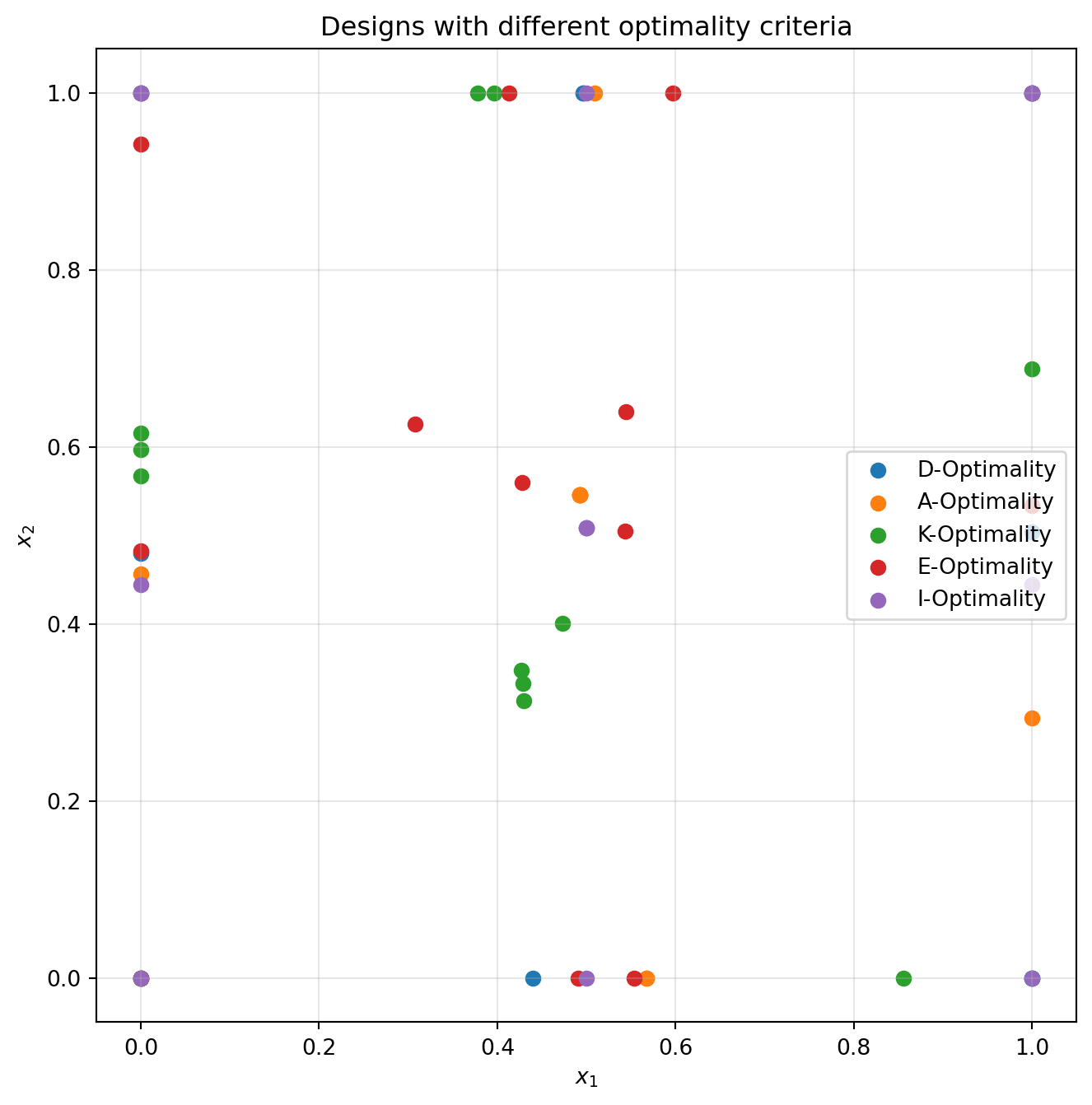
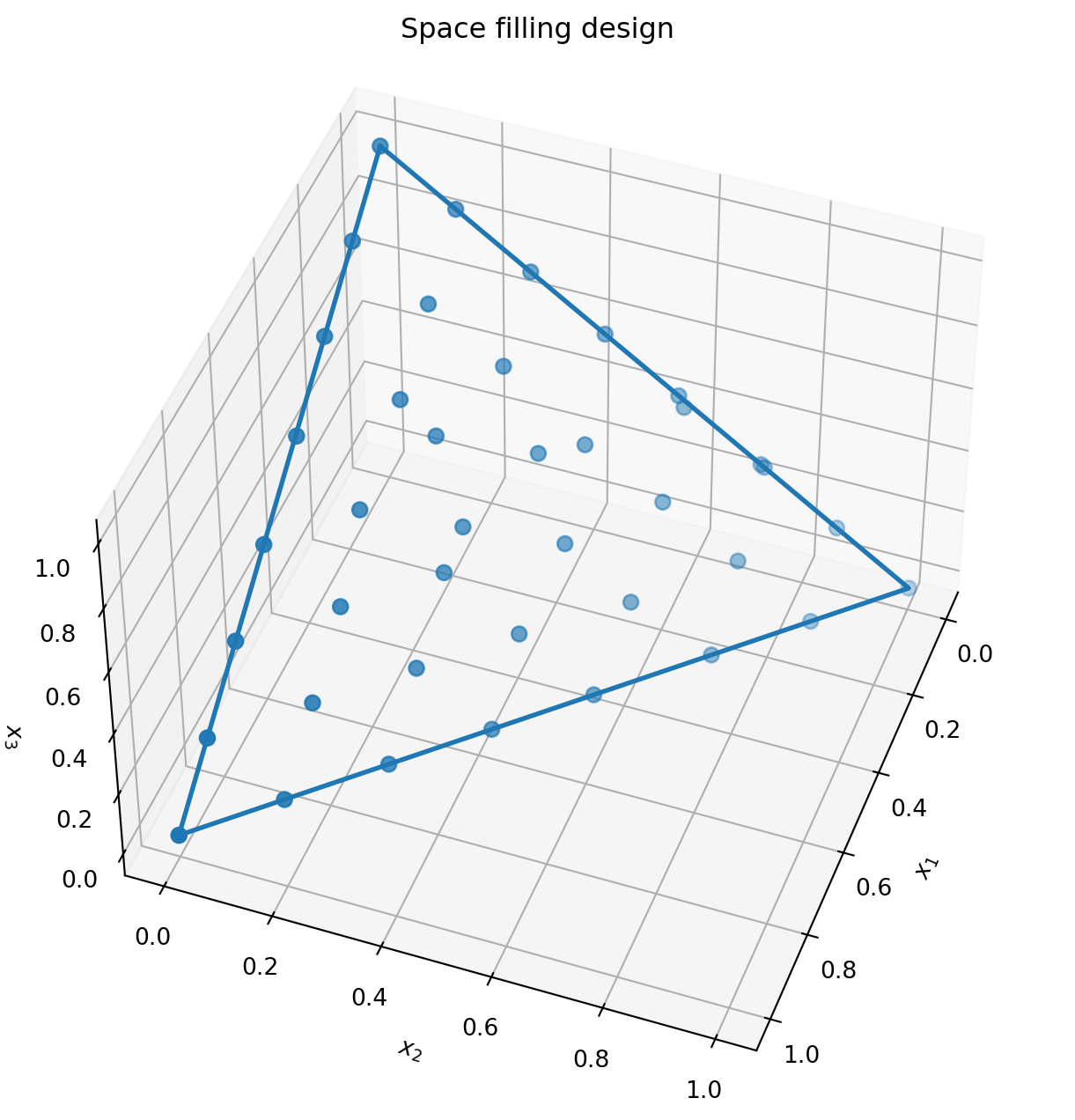
Space filling design
BoFire can also generate space filling designs, here it is show three dimensions and a simplex constraint.
# Space filling design on the unit 2-simplex
domain = Domain(
inputs=[ContinuousInput(key=f"x{i+1}", bounds=(0, 1)) for i in range(3)],
outputs=[ContinuousOutput(key="y")],
constraints=[
LinearEqualityConstraint(
features=["x1", "x2", "x3"],
coefficients=[1, 1, 1],
rhs=1,
),
],
)
data_model = DoEStrategy(
domain=domain, criterion=SpaceFillingCriterion(), ipopt_options={"max_iter": 500}
)
strategy = strategies.map(data_model=data_model)
X = strategy.ask(candidate_count=40).to_numpy()
fig = plt.figure(figsize=((10, 8)))
ax = fig.add_subplot(111, projection="3d")
ax.view_init(45, 20)
ax.set_title("Space filling design")
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$x_3$")
# plot feasible polytope
ax.plot(xs=[0, 0, 1, 0], ys=[0, 1, 0, 0], zs=[1, 0, 0, 1], linewidth=2)
# plot design points
ax.scatter(xs=X[:, 0], ys=X[:, 1], zs=X[:, 2], s=40)
plt.show()